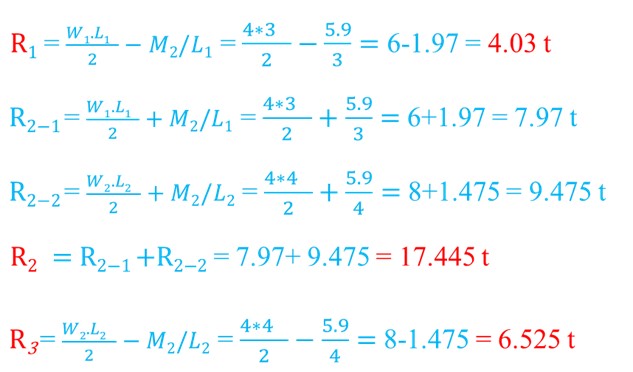حساب وتصميم المنشآت البيتونية المسلحة (3) - الواحة الأكاديمية للجامعة الوطنية الخاصة

الجامعــة الوطنيــة الخاصــة

Al-Wataniya Private University

الواحة الأكاديمية للجامعة الوطنية الخاصة

حساب وتصميم المنشآت البيتونية المسلحة (3)

الجوائز المستمرة (3)

طريقة معادلة العزوم الثلاثة (كلابيرون)

أولاً : مبدأ الطريقة.

نوضح مبدأ الطريقة من خلال المثال التالي:

لدينا جائز مستمر مؤلف من n فتحة ومحمل بحمولات مختلفة ومتنوعة.

انه منشأة غير مقررة من الدرجة الثالثة. ولحله بطريقة المرونة يتم تقريره عادة على الشكل التالي:

ويتم رسم منحني الخط المرن له على الشكل التالي:

ندرس الجزء منه الواقع بين المساند الثلاثة 1 و 2 و 3 . ويكون انتقالها y3 , y2 , y1 على الترتيب.

وتكون الحالة الإجهادية ناتجة عن الانتقال التفاضلي y حيث :

y = y2-y’-y’’

ومن تشابه المثلثات يكون:

y = y2-y1.L2/(L2+L1) – y3.L1/(L2+L1) (1)

من ناحية أخرى فإن الانتقال يساوي تكامل ثنائي للعزم مقسوما على EI , أي :

𝑦= ∬(𝑀/𝐸𝐼) 𝑑𝑥,

وقد قام المهندس Clapeyron عام 1857 بإجراء هذا التكامل بيانياً على الشكل التالي:

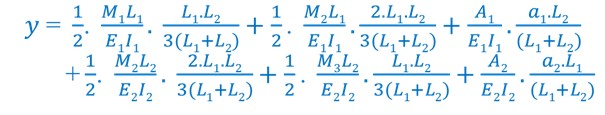
حيث: A1مساحة مخطط العزم للجائز البسيط L1 و a1 بعد مركز ثقله عن المسند .1

A2 مساحة مخطط العزم للجائز البسيط L2 و a2 بعد مركز ثقله عن المسند 3.

بالتعويض في العلاقة السابقة (1) يكون:

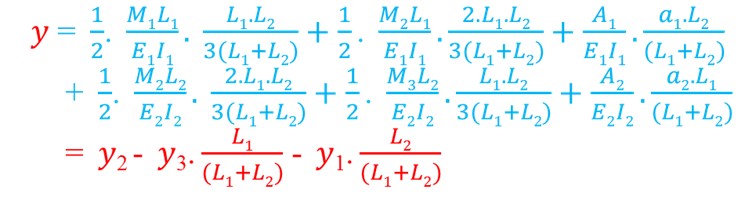
نفرض عامل المرونة E ثابت على جميع الفتحات. ونصلح العلاقة بضربها بالمقدار

(6E(L1+L2)/(L1.L2

فيكون :

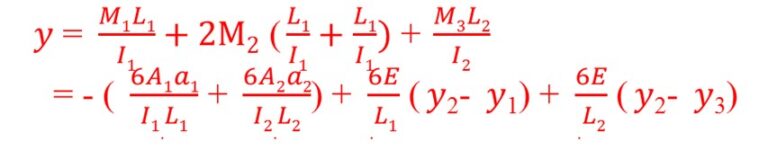
وهذ ما يسمى بمعادلة العزوم الثلاثة أو طريقة كلابيرون.

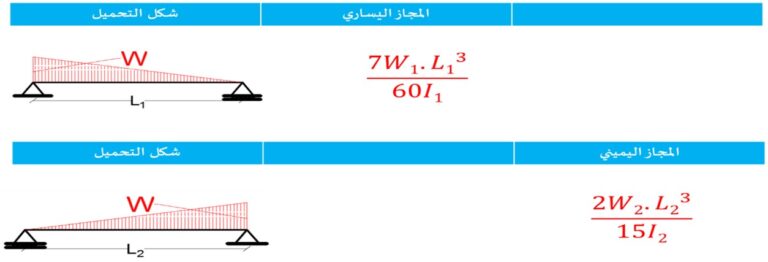
في الجدول التالي يبين قيمة A و a لكل حالة تحميل (مساحة مخطط العزم وبعد مركز ثقله عن المسند الطرفي الموافق) :

في الجدول التالي يبين قيمة

6𝐴2𝑎2/(𝐿2.𝐼2) , 6𝐴1𝑎1/(𝐿1.𝐼1)

لكل حالة تحميل :

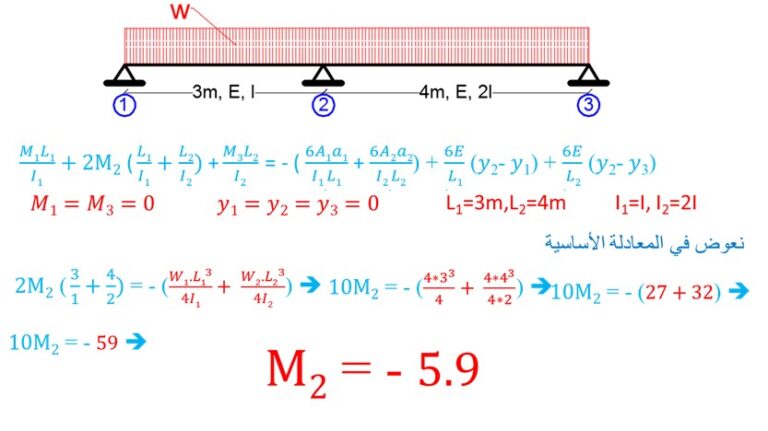
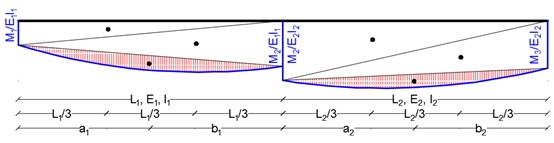
مثال (1)

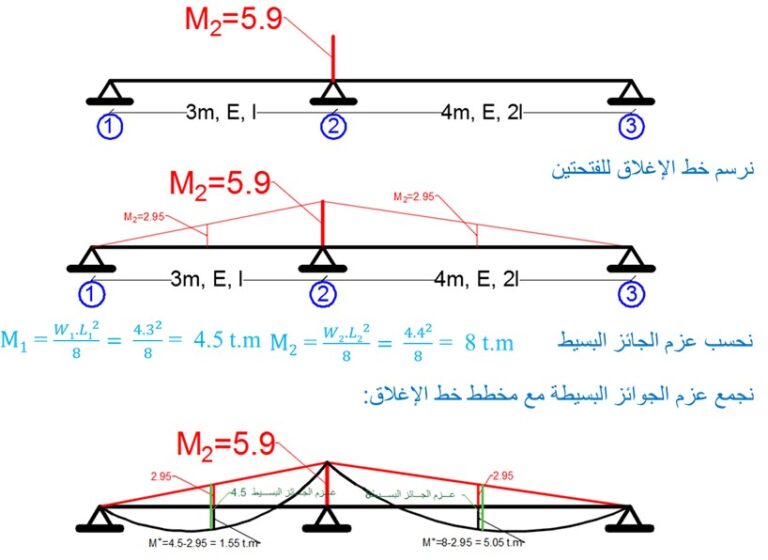
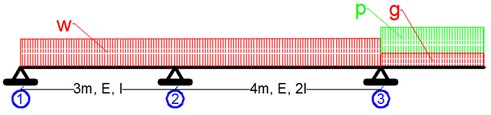
أرسم مخطط عزوم الانعطاف للجائز المبين أدناه :

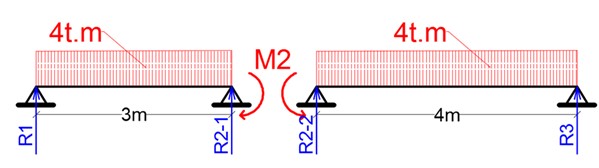
لحساب ردود الأفعال نقسم الجائز الى جائزين بسيطين كما يلي :

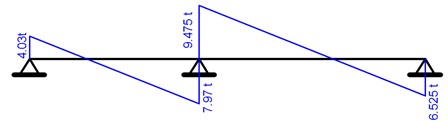
فنحصل على مخطط ردود الأفعال كما يلي :

ونرسم مخطط قوى القص كمايلي :

في حالة وجود ظفر:

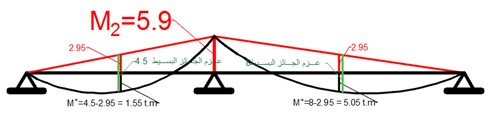
نتجاهل وجود الظفر ونعالج الجائز حتى الوصول الى مخطط العزم.

ونعيد الظفر الى مكانه بعد رسم مخطط العزم للحمولات الميتة وللحمولات الكلية.

نعدل مخطط العزم بما يتناسب مع خط الإغلاق للحمولات الميتة فقط .

الجامعة الوطنية الخاصة

تأسست عام 2007 و تضم ست كليات :

مواقع مرتبطة:

للتواصل :

تنفيذ إدارة المواقع الالكترونية في الجامعة الوطنية الخاصة 2023