الجامعــة الوطنيــة الخاصــة
Al-Wataniya Private University
الواحة الأكاديمية للجامعة الوطنية الخاصة
- الرئيسية
- مقالات علمية لكلية الهندسة المدنية
- أبحاث علمية لكلية الهندسة المدنية
- السير العلمية
نظرية العزوم الثلاث (معادلة كلابيرون)
- مقدمة
سنعرض في هذه المقالة شرحاً مختصراً لاستخدام طريقة معادلة العزوم الثلاث في حساب القوى الداخلية الناتجة عن تحميل الجوائز المستمرة بمختلف حالاتها. والشرح الكامل لهذه الطريقة مع أمثلة محلولة موجود تحت الرابط () .
الكلمات المفتاحية: نظرية العزوم الثلاث, معادلة كلابيرون, الجوائز المستمرة, طريقة القوى.
- طريقة العزوم الثلاثة:
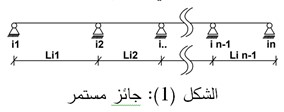
تعتبر طريقة العزوم الثلاث (معادلة كلابيرون Clapeyron) حالة خاصة من طريقة العمل الوهمي (طريقة القوى) المستخدمة في حساب وتحليل المنشآت غير المقررة, وتستخدم بشكل خاص لحساب وتحليل الجوائز المستمرة, حيث يُعرّف الجائز المستمر بأنه جائز يستند على أكثر من مسندين بشرط أن لا يقطع مادته أي مفصل والمجاهيل فيه هي العزوم عند المساند الشكل (1).
للحصول على معادلة العزوم الثلاث يجب أولاً تقرير الجائز وذلك بإدخال مفاصل عند المساند فتكون المجاهيل هي قيم العزوم المحررة في المساند نتيجة ادخال المفاصل الشكل (2).
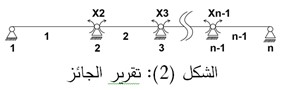
ويكون عدد المعادلات المستخرجة مساوياً لعدد المجاهيل وكل معادلة منها تحتوي على ثلاث مجاهيل (العزوم الثلاثة) عدا المعادلتين الأولى والأخيرة حيث تحوي كل منهما على مجهولين فقط. ويجب أثناء تقرير الجائز أخذ الملاحظات التالية بعين الاعتبار:
ملاحظة 1: إذا كان المسند الطرفي في الجائز وثاقة وليكن المسند A فسيكون الجائز مستمر عند A بحكم الوثاقة وذلك لوجود عزم فيه, وهنا تُمثَّل الوثاقة بفتحة واقعة على يسار المسند طولها وعزم عطالة مقطعها لا متناهي أي كما في الشكل (3-a).
ملاحظة 2: وإذا كانت نهاية الجائز عبارة عن ظفر فيُحذف الظفر ويحمل الجائز عند مسنده الأخير بعزم يساوي العزم الناتج عن تحميل الظفر مع مراعاة اشارة العزم الشكل (3-b).

ملاحظة 3: يعتبر العزم موجب إذا أحدث اجهادات شد في الألياف السفلية للجائز وسالب بالعكس وتؤخذ هذه الاشارة بعين الاعتبار عند حساب مساحة مخططات العزوم.
1.2 المعادلات الأساسية لنظرية العزوم الثلاث:
ليكن لدينا الجائز المستمر المستند استناداً بسيطاً من طرفيه وعدد فتحاته n. يتم تقرير الجائز بإدخال مفاصل عند نقاط الاستناد كما في الشكل (4)

ويكون لدينا (n-1) مجهول (المجاهيل هنا هي عزوم المساند في الجائز) ولإيجاد هذه المجاهيل نحتاج إلى (n-1) معادلة. ولإيجاد المعادلات المطلوبة ننطلق من حقيقة أن الدورانات النسبية فوق مساند الجائز الفعلي معدومة, ولضبط سلوكية الجائز المقرر مع الجائز الفعلي يجب أن تكون الدورانات فوق مساند الجائز المقرر أيضاً معدومة, وبالتالي يمكن كتابة معادلات الحل بالشكل , حيث تعبر عن قيمة الدوران النسبي الكلي عند المسند i في الجائز المقرر تحت تأثير كافة الأحمال, وتكون معادلة التوازن للجائز المقرر من الشكل , ووفقاً لطريقة العمل الوهمي يكون:
δ_i1*X1+δ_i2*X2+⋯+δ_i(i-1) 〖*X〗_((i-1) )+δ_ii*Xi+δ_i(i+1) 〖*X〗_((i+1) )+⋯+δ_in Xn+θ_ip=0
وتعني هذه المعادلة بأن الدوران النسبي الكلي فوق المسند i الناتج عن تأثير جميع المجاهيل من حتى (والتي هي قيم العزوم عند مساند الجائز) إضافة إلى الحمل الخارجي مساوٍ للصفر حيث:
– : الدوران النسبي فوق المسند i تحت تأثير العزم الواحدي المطبق في المسند .
– : تمثل الدوران النسبي الحقيقي فوق المسند i الناتج عن تأثير العزم الحقيقي المطبق في المسند .
– : الدوران النسبي فوق المسند i اناتج عن تأثير الحمولات الخارجية على الفتحة Li.
تُحسب الأمثال δ وفق العلاقة (2) والحد الحر θ_ip وفق العلاقة (3) التاليتين:
δ_i(i-1) =∫_s▒〖¯M_i.□(¯M_((i-1))/(E.I_(i-1) )).〗 d_x (2) , θ_ip=∫_s▒〖¯M_i.□(M_p/(E.I)).〗 d_x (3)
حيث : ¯M_i : مخطط العزم الواحدي الناتج عن تطبيق عزم واحدي Xi =1 في المسند i.
¯M_((i-1)) : مخطط العزم الواحدي الناتج عن تطبيق عزم واحدي Xi-1=1 في المسند (i-1).
Mp : مخطط العزم الناتج عن الحمولات الخارجية باعتبار الفتحة تستند استناداً بسيطاً.
لحساب الأمثال δ_in يتم رسم مخططات العزوم الواحدية في الجملة المقررة للفتحتين Li+1 و Li وذلك باعتبار كل فتحة تعمل كجائز بسيط وبتطبيق المعادلة (2) والاختصار نحصل على:
لحساب الأمثال δ_in يتم رسم مخططات العزوم الواحدية في الجملة المقررة للفتحتين Li+1 و Li وذلك باعتبار كل فتحة تعمل كجائز بسيط وبتطبيق المعادلة (2) والاختصار نحصل على:
δ_ii=∫_s▒〖¯M_i.□(¯M_i/(E.I_i )).〗 d_x=1/3*(l_i/(EI_i )+l_(i+1)/(EI_(i+1) )) , δ_i(i-1) =∫_s▒〖¯M_i.□(¯M_((i-1))/(E.I_(i-1) )).〗 d_x=1/6*l_i/(EI_i )
δ_i(i+1) =∫_s▒〖¯M_i.□(¯M_((i+1))/(E.I_(i+1) )).〗 d_x=1/6*l_(i+1)/(EI_(i+1) )
وكذلك لحساب الأمثال θ_ip يتم رسم مخطط العزم Mp للحمولات الخارجية لكل فتحة من فتحات الجائز على حدة باعتبارها جائزاً بسيطاً كما في الشكل (5).
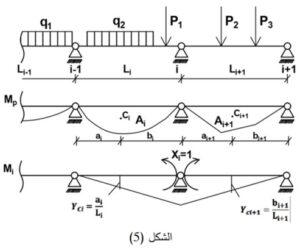
وباعتبار أن: Ai , Ai+1 مساحة مخطط العزم Mp للحمولات الخارجية المؤثرة في الجائز Li+1 وLi .
Ci , Ci+1 تمثل مركز ثقل المساحة Ai+1 وAi .
ai بعد مركز ثقل مخطط المساحة Ai عن المسند i-1.
bi+1 بعد مركز ثقل مخطط المساحة Ai+1 عن المسند i+1.
yi , yi+1 الترتيب من مخطط عزم القوى الواحدية ¯M_i المقابل لمركز ثقل المساحة Ai+1 ,Ai .
وبتطبيق المعادلة (3) والاختصار يكون:
θ_ip=∫_s▒〖M_i.□(M_p/(E.I)).〗 d_s=A_c 〖*Y〗_c*1/EI=A_i*□(a_i/l_i )*1/(EI_i )+A_(i+1)*□(b_(i+1)/l_(i+1) )*1/(EI_(i+1) )
وبالتعويض في المعادلة الأساسية (1) وباعتبار قيمة E ثابتة على طول الجائز نحصل على:
l_i/I_i *X_(i-1)+2*(l_i/I_i +l_(i+1)/I_(i+1) )*X_i+l_(i+1)/I_(i+1) *X_(i+1)=-6*[A_i/I_i *□(a_i/l_i )+A_(i+1)/I_(i+1) *□(b_(i+1)/l_(i+1) )]
وهي معادلة العزوم الثلاث للفتحتين Li+1 و Li, ولتبسيط الأمور يتم تسمية المساند (i-1), (I) و (i+1) بــA B, و C كما في الشكل التالي وباستبدال الرموز في المعادلة السابقة بالرموز الجديدة تصبح المعادلة كما يلي:
〖 M〗_A=X_(i-1) , l_AB=l_i ,
M_B=X_i , l_BC=l_(i+1) ,
M_C=X_(i+1) ⇒┴
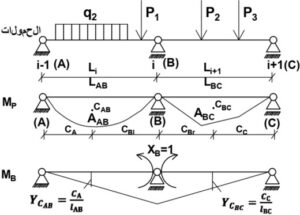
M_A.l_AB/I_AB +2.M_B (l_AB/I_AB +l_BC/I_BC )+M_C.l_BC/I_BC =-6(A_AB/I_AB .C_A/l_AB +A_BC/I_BC .C_C/l_BC )
حيث: – A_AB مساحة مخطط العزم للفتحة ِAB – C_A بعد مركز ثقل مخطط A_AB عن المسند A.
– A_BC مساحة مخطط العزم للفتحة BC – C_C بعد مركز ثقل مخطط A_BC عن المسند C.
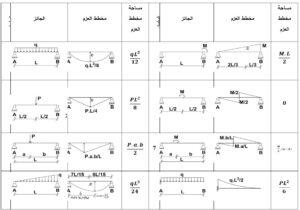
حيث A_AB وA_BC تحسب يدوياً أو تؤخذ من جداول خاصة لبعض المخططات كما في الجدول (1).
و بفرض أن: B=A_BC.C_C/l_BC , A=A_AB .C_A/l_AB
تصبح المعادلة السابقة بالشكل:
M_A.l_AB/I_AB +2.M_B (l_AB/I_AB +l_BC/I_BC )+M_C.l_BC/I_BC ==-6*(A/I_AB +B/I_BC ) (5)
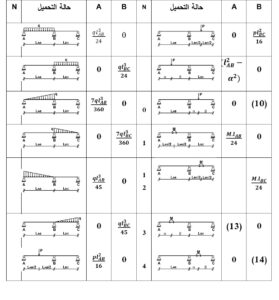
وهي الصيغة العامة لمعادلة العزوم الثلاث (أو ما يسمى معادلة كلابيرون). وتعطى القيم A وB وفقاً لشكل الحمولة الخارجية في الجدول (2).
أثناء الحل يتم تطبق معادلة العزوم الثلاث على فتحات الجائز بالتتالي, فمثلاً إذا كان الجائز مكوناً من أربع فتحات و يستنداً على المساند A, B, C, D, E, F فيتم الحل بتطبيق المعادلة على فتحاته وفق الترتيب التالي: نطبق المعادلة أولاً على الفتحتين A, B, C وتكون المجاهيلMB, MC حيث MA=0 فنحصل على المعادلة الأولى للحل ثم نطبق المعادلة على الفحتين B, C, D وتكون المجاهيل هنا MB, MC, MD ونحصل على المعادلة الثانية ثم نطبق المعادلة على الفحتين C, D, E وتكون المجاهيل هناMC, MD, ME ونحصل على المعادلة الثالثة ثم نطبق المعادلة على الفحتين D, E, F وتكون المجاهيل هناMD, MF وتكون MF=0 ونحصل على المعادلة الرابعة للحل وبهذا نكون قد حصلنا على أربع معادلات بأربعة مجاهيل (هي العزوم في المساند الوسطية للجائز) وبحلها نحصل على عزوم المساند في الجائز.
وتحت الرابط التالي (…) نجد شرحاً مفصلاً لهذه الطريقة يتضمن الجداول التابعة لها وأمثلة عملية محلولة.
الجدول (1) مساحات بعض أشكال مخططات العزوم وبعد مراكز ثقلها عن المساند.
M_A.l_AB/I_AB +2.M_B (l_AB/I_AB +l_BC/I_BC )+M_C.l_BC/I_BC =-6(A_AB/I_AB .C_A/l_AB +A_BC/I_BC .C_C/l_BC )
الجدول (2): قيم A و B المستخدمة في معادلة العزوم الثلاثة لبعض حالات التحميل الممكنة:
M_A.l_AB/I_AB +2.M_B (l_AB/I_AB +l_BC/I_BC )+M_C.l_BC/I_BC ==-6*(A/I_AB +B/I_BC )
(10): (p.β)/(〖6.l〗_BC^ ) 〖.(l〗_BC^2-β^2), (13): M/(l_AB^2 ).[2.α^3-β^2.(3.α+β)] , (14): M/(l_BC^2 ).[α^2.(3.α+β)-2.β^3]
المراجع:
- حساب الإنشاءات 1 , الدكتور المهندس نبيل نادر 1981-1982 جامعة تشرين.
- ميكانيك الإنشاءات 1, الدكتور عصام ناصر 1994-1995, جامعة تشرين.
- محاضرات ميكانيك الإنشاءات 1, الدكتور رفيع مهنا, جامعة دمشق.
- تحليل المنشآت اللامقررة, الدكتور المهندس محمد عارف المهايني و المهندس محمد فاروق الزين, 1981.
- ميكانيك الإنشاءات, المهندس صفوان الطويل.
- الميكانيكا الإنشائية, أ. داركوف, ف. كوزنيتسوف, دار مير للطباعة و النشر, 1980.
الجامعة الوطنية الخاصة
مواقع مرتبطة:
للتواصل :
- سوريا - محافظة حماة - الطريق الدولي حمص حماة
- 0096334589094
- 00963335033
- info@wpu.edu.sy